Break-even charts

In nearly all businesses, there is a close correlation between the level of turnover and the profit or loss.

The managers should know that if invoiced sales reach a certain figure the business will break even.

If invoiced sales are above that figure the business will be in profit.

The break-even point depends on the relationship between the fixed and the variable (or direct) costs.


Breakeven chart. 



The break-even point can be calculated by drawing a graph showing how fixed costs, variable costs, total costs and total revenue change with the level of output.


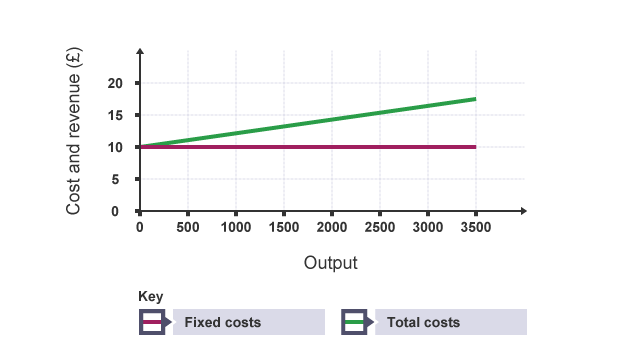
Fixed costs are shown as a flat line in the chart above..

The total costs are the result of adding the variable costs to the fixed costs.

The revenue is the result of sales.

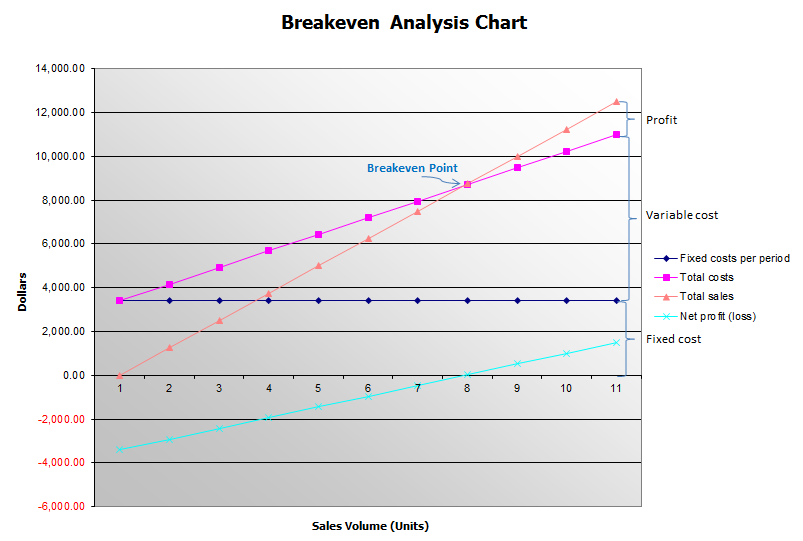
The break-even point is when the total costs line crosses the revenue line.  It is at this point where these lines cross.

Profit and loss can also be read from the chart.

In practice, the relationships are rarely quite so straightforward, as some of the costs may be semi-variable.




More charts:

Warrants: Premium

Premium is a measure of how much the underlying price has to move for the warrant to break even if it is held until maturity.

The premium for a call warrant

= [Strike Price + (Warrant Price x Conversion Ratio) - Underlying Price] x 100% / Underlying Price


(1)  Cost of buying a warrant = Warrant Price x Conversion Ratio
(2)  Breakeven point of the warrant = Strike Price  + Cost of component
(3)  Premium = [(Breakeven point of warrant - Underlying Price ) / Underlying Price]  x 100%


In this formula, we first calculate the difference between the breakeven point and the underlying price and then divided it by the underlying price to find out the premium as a percentage.


Likewise, the premium for a put warrant 

= {Underlying Price - [Strike Price - (Warrant Price x Conversion Ratio)]} x 100% / Underlying Price


For example:

Company ABC Call Warrant currently trading at $0.54, with a strike price of $12 and a conversion ratio of 5:1.  If the underlying price is $14, how much is the premium?

Cost of buying the warrant = $0.54 x 5 = $2.70
Breakeven point = Strike Price + Cost = $12 + $2.70 = $14.70
Underlying price = $14.00
Difference between Underlying price and Breakeven point = $14.70 - $14,00 = $0.70
Premium = ($0.70/$14.00) x 100%  = 5%.

In other words, if the investor intends to hold the warrant until maturity, it takes a 5% increase in the underlying price from its current level of $14 to breakeven.

In this example, what we have is an out-of-the-money (OTM) warrant, and the underlying must make a bigger climb to reach the breakeven point.

In the case of an in-the-money (ITM) warrant, a modest increase in the underlying price would be enough.




Summary:

Step 1:   First, calculate the breakeven point of the warrant. This is done by using the formula:  [(price of warrant x conversion ratio) + strike price]

Step 2:  Work out the difference between the breakeven point and underlying price and divide this by the underlying price to get the premium in percentages.



The premium only measures the percentage increase in the underlying price that will allow the warrant investor to break even upon maturity.

It does not tell us whether the price of a warrant is too high or too low.

Hence, unless you are prepared to hold the warrant until maturity, premium is not a relevant indicator for you.